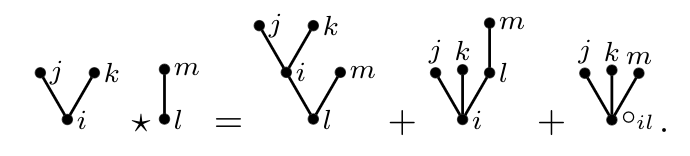Enzo Miller

Enzo Miller

PhD student in stochastic control

A general method for explicit solution of (non markovian) control problem (In progress)

less than 1 minute read

Published:

In this post, we are going to talk about a very easy to use general method to solve (non markovian) control problem explicitly, provided some algebraic assumptions on the structure of the dynamic and cost functional are satisfied. As explained below, the method allows us to find explicit solutions which might be usefull in the to benchmark RL algorithm on various non markovian problems. The goal here is to make an easy to read presentation, for more details I have linked the technical papers when they exist !

Table of contents

  1. Reminder on the classical (markovian) Linear-Quadratic case
  2. [Dynamic with delays]Link to paper
  3. Volterra case (rough noise, fractional Brownian motion, etc)
    1. [Convolution type] (See this paper)
    2. [Non convolution type] (unpublished yet)
  4. On the use of the signature : a general linearization on the path space(unpublished yet)

You May Also Enjoy

Neural network and stochastic control (In progress)

less than 1 minute read

Published:

In this post, we are going to see how to use neural network to solve optimal (or stochastic) control problems. The use of deep learning to such task is quite recent in in the control community, see this paper or this one to name just a few; and as you’ll see, its approach differs quite a bit from the one we are used to see in the reinforcement learning community.

Solving differential equations with neural nets

less than 1 minute read

Published:

This notebook gives a minimal starter code to solve any differential equation with any constraint. Note that the dimension of the problem tackled here is only 2, which would be easily solved by standart methods. But were the dimension be several hundreds, every classical methods would breakdown ! The reason being the exponential size of the mesh that would be needed with euler schemes and similar methods.

A short introduction to optimal control

12 minute read

Published:

This is a very non-mathematical and straightforward presentation of what is optimal control. The goal is to see :

  1. What it is mainly about,
  2. Some ideas to solve the problems we are about to see.